عدد عقدي
من ويكيبيديا، الموسوعة الحرة
العدد المركب: (Complex number) هو أي عدد يُكتب على الصورة  حيث
حيث  و
و  عددان حقيقيان و
عددان حقيقيان و  عدد خيالي مربعه يساوي 1- (أي أن i² = -1) ويسمى وحدة تخيلية. ويسمي العدد الحقيقي
عدد خيالي مربعه يساوي 1- (أي أن i² = -1) ويسمى وحدة تخيلية. ويسمي العدد الحقيقي  بالجزء الحقيقي، والعدد الحقيقي
بالجزء الحقيقي، والعدد الحقيقي  بالجزء التخيلي. فمثلا، 3 + 2i هو عدد مركب، فيه 3 هو الجزء الحقيقي و 2 هو الجزء التخيلي.
بالجزء التخيلي. فمثلا، 3 + 2i هو عدد مركب، فيه 3 هو الجزء الحقيقي و 2 هو الجزء التخيلي.
 حيث
حيث  و
و  عددان حقيقيان و
عددان حقيقيان و  عدد خيالي مربعه يساوي 1- (أي أن i² = -1) ويسمى وحدة تخيلية. ويسمي العدد الحقيقي
عدد خيالي مربعه يساوي 1- (أي أن i² = -1) ويسمى وحدة تخيلية. ويسمي العدد الحقيقي  بالجزء الحقيقي، والعدد الحقيقي
بالجزء الحقيقي، والعدد الحقيقي  بالجزء التخيلي. فمثلا، 3 + 2i هو عدد مركب، فيه 3 هو الجزء الحقيقي و 2 هو الجزء التخيلي.
بالجزء التخيلي. فمثلا، 3 + 2i هو عدد مركب، فيه 3 هو الجزء الحقيقي و 2 هو الجزء التخيلي.
و عندما يكون "b" (أي الجزء التخيلي) مساوياً ل 0، فإن قيمة العدد المركب تساوي قيمة الجزء الحقيقي "a" فقط ، ويسمي العدد عددًا حقيقيـًا صرفًا. وعندما يكون "a" (أي الجزء الحقيقي) مساويا ل 0، يكون العدد تخيليـًا صرفـًا.
من الممكن إجراء العمليات الحسابية العادية على الأعداد المركبة كالجمع والطرح والضرب والقسمة بطريقة تماثل الأعداد الحقيقية مع بعض الاختلافات خاصةً في عملية القسمة. ولكنها أيضـًا تتمتع بخصائص أخرى تمكنها من حل كافة المعادلات الجبرية العادية التي يصعب حلها باستخدام الأعداد الحقيقية فقط.
عندما وجد الرياضيون أن المعادلة (x² = -1) مستحيلة الحل في مجموعة الأعداد الحقيقية كان لا بد من وضع حل لها. وبما أن الرياضيات هي -وكما يقول أحد الرياضياتيين- العلم الذي لا نعرف فيه إن كان ما نقوله صحيحا أم لا، لذلك تمّ إيجاد عدد جديد هو العدد التخيلي i. وتعريف العدد i هو الجذر التربيعي للعدد -1. وهنا يكمن التعقيد. فمن المعلوم أنه ليس للعدد -1 جذر تربيعي، ولكن هذا في الأعداد الحقيقية. فكما أنه لا وجود للعدد -5 في الأعداد الطبيعية ولكنه موجود في الأعداد الصحيحة (والحال نفسه بالنسبة للعدد i) فالرياضيات هي علم وضعه البشر ولهم الحق في تطويره وتجديده وفق قواعد واضحة تخضع للمنطق الرياضي ولا تنافي المبادئ الرياضية والموضوعات والبديهيات في علم الرياضيات.
نظرة شاملة
تمنح الأعداد العقدية حلولا لبعض الأنواع من المعادلات التي لا تقبل أية حلول في مجموعة الأعداد الحقيقية : المعادلة
لا تقبل أي حل حقيقي لأن مربع عدد حقيقي إما يساوي الصفر أو هو موجب. الأعداد المركبة تمنح حلا لهاته المعضلة. الفكرة هي تمديد الأعداد الحقيقية بالوحدة التخيلية i حيث  , مما يمكن من إيجاد حل للمعادلة السابقة. في هذه المعادلة الحل هو −1 ± 3i. هكذا، ليس فقط تصبح جميع المعادلات التربيعية ذات المتغير الواحد قابلة للحلحلة، بل أيضا، تصبح جميع المعادلات الحدودية ذات المتغير الواحد قابلة للحلحلة باستعمال الأعداد العقدية.
, مما يمكن من إيجاد حل للمعادلة السابقة. في هذه المعادلة الحل هو −1 ± 3i. هكذا، ليس فقط تصبح جميع المعادلات التربيعية ذات المتغير الواحد قابلة للحلحلة، بل أيضا، تصبح جميع المعادلات الحدودية ذات المتغير الواحد قابلة للحلحلة باستعمال الأعداد العقدية.
 , مما يمكن من إيجاد حل للمعادلة السابقة. في هذه المعادلة الحل هو −1 ± 3i. هكذا، ليس فقط تصبح جميع المعادلات التربيعية ذات المتغير الواحد قابلة للحلحلة، بل أيضا، تصبح جميع المعادلات الحدودية ذات المتغير الواحد قابلة للحلحلة باستعمال الأعداد العقدية.
, مما يمكن من إيجاد حل للمعادلة السابقة. في هذه المعادلة الحل هو −1 ± 3i. هكذا، ليس فقط تصبح جميع المعادلات التربيعية ذات المتغير الواحد قابلة للحلحلة، بل أيضا، تصبح جميع المعادلات الحدودية ذات المتغير الواحد قابلة للحلحلة باستعمال الأعداد العقدية.تعريف
عدد مركب هو عدد يُكتب على الشكل التالي :
حيث a و b عددان حقيقيان و i هي الوحدة التخيلية, وتحقق i2 = −1. على سبيل المثال،  هو عدد عقدي. عادة، يُشار إلى العدد العقدي
هو عدد عقدي. عادة، يُشار إلى العدد العقدي  ب a وإلى العدد العقدي
ب a وإلى العدد العقدي  ب
ب  . بالإضافة إلى ذلك، عندما يكون الجزء التخيلي سالبا، يكتب العدد العقدي على شكل
. بالإضافة إلى ذلك، عندما يكون الجزء التخيلي سالبا، يكتب العدد العقدي على شكل  حيث b موجب بدلا من
حيث b موجب بدلا من  . على سبيل المثال، يُكتب
. على سبيل المثال، يُكتب  بدلا من
بدلا من  .
.
 هو عدد عقدي. عادة، يُشار إلى العدد العقدي
هو عدد عقدي. عادة، يُشار إلى العدد العقدي  ب a وإلى العدد العقدي
ب a وإلى العدد العقدي  ب
ب  . بالإضافة إلى ذلك، عندما يكون الجزء التخيلي سالبا، يكتب العدد العقدي على شكل
. بالإضافة إلى ذلك، عندما يكون الجزء التخيلي سالبا، يكتب العدد العقدي على شكل  حيث b موجب بدلا من
حيث b موجب بدلا من  . على سبيل المثال، يُكتب
. على سبيل المثال، يُكتب  بدلا من
بدلا من  .
.
رمز مجموعة الأعداد العقدية هو 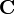 أو
أو  .
.
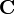 أو
أو  .
.
العدد الحقيقي a الذي يظهر في تعريف العدد العقدي z = a+ bi يسمى الجزء الحقيقي ل z، بينما يسمى b الجزء التخيلي ل z. هكذا، الجزء التخيلي لعدد عقدي ما، هو عدد حقيقي (لا يتضمن الوحدة التخيلية) : الجزء التخيلي ل z هو b وليس bi. يُرمز للجزء الحقيقي ب (Re(z أو (ℜ(z, ويُرمز إلى الجزء التخيلي ب (Im(z أو (ℑ(z. على سبيل المثال،,
أحيانـًا, يُكتب العدد المركب z على الصورة z = a + bj (خصوصـًا في مجال الهندسة الكهربية، وذلك باستخدام الرمز "j" بدلا من "i"، لأن "i" هو رمز التيار الكهربي)
العمليات الأساسية
نفس العمليات والقواعد الحسابية في الأعداد الحقيقة  يمكن تطبيقها على الأعداد المركبة. باستعمال تجميعية الجمع وتوزيعية الضرب نحصل على ما يلي:
يمكن تطبيقها على الأعداد المركبة. باستعمال تجميعية الجمع وتوزيعية الضرب نحصل على ما يلي:
 يمكن تطبيقها على الأعداد المركبة. باستعمال تجميعية الجمع وتوزيعية الضرب نحصل على ما يلي:
يمكن تطبيقها على الأعداد المركبة. باستعمال تجميعية الجمع وتوزيعية الضرب نحصل على ما يلي:مرافق عدد مركب
مرافق العدد المركب  هو العدد المركب
هو العدد المركب  . يُرمز لمرافق العدد المركب
. يُرمز لمرافق العدد المركب  بالرمز
بالرمز 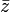 . هندسيا،
. هندسيا، 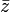 هو انعكاس
هو انعكاس  حول محور الأعداد الحقيقية. هكذا محاولة الحصول على مرافق مرافق عدد مركب ما تعطي العدد ذاته :
حول محور الأعداد الحقيقية. هكذا محاولة الحصول على مرافق مرافق عدد مركب ما تعطي العدد ذاته :  .
.
 هو العدد المركب
هو العدد المركب  . يُرمز لمرافق العدد المركب
. يُرمز لمرافق العدد المركب  بالرمز
بالرمز 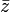 . هندسيا،
. هندسيا، 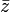 هو انعكاس
هو انعكاس  حول محور الأعداد الحقيقية. هكذا محاولة الحصول على مرافق مرافق عدد مركب ما تعطي العدد ذاته :
حول محور الأعداد الحقيقية. هكذا محاولة الحصول على مرافق مرافق عدد مركب ما تعطي العدد ذاته :  .
.
يمكن أن يستخلص الجزءان الحقيقي والتخيلي انطلاقا من مرافق عدد مركب ما، كما تبين المعادلتان التاليتان :
بالإضافة إلى ذلك، فإن عددا مركبا ما حقيقيٌ إذا وفقط إذا كان مساويا لمرافقه.
البحث عن المرافق يتوزع على العمليات الحسابية الاعتيادية كما تبين المعادلات التالية:
 أي أن مرافق مجموع عددين مركبين هو مجموع مرافق كل من حدي المجموع.
أي أن مرافق مجموع عددين مركبين هو مجموع مرافق كل من حدي المجموع. أي أن مرافق حاصل ضرب عددين مركبين هو حاصل ضرب المرافقين لهذين العددين.
أي أن مرافق حاصل ضرب عددين مركبين هو حاصل ضرب المرافقين لهذين العددين. أي أن مرافق حاصل قسمة عددين مركبين هو حاصل قسمة المرافقين لهذين العددين.
أي أن مرافق حاصل قسمة عددين مركبين هو حاصل قسمة المرافقين لهذين العددين.
مقلوب عدد مركب ما مختلف عن الصفر  ، هو :
، هو :
 ، هو :
، هو :
لاحظ أن ناتج عملية القسمة السابقة نحصل عليه بضرب كلا من البسط والمقام في العدد المرافق للمقام.
الجذر التربيعي لحاصل ضرب عدد مركب في مرافقه يسمى معيار العدد المركب.
الجمع والطرح
تتم عملية الجمع كما يلي: 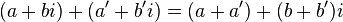
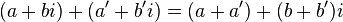
وكذلك عملية الطرح كما يلي: 

يلاحظ أن الجزء الحقيقي للناتج هو محصلة الجزئين الحقيقيين للعددين، وبالمثل الجزء التخيلي للناتج هو محصلة الجزئين التخيليين للعددين.
الضرب والقسمة
تتم عملية الضرب كما يلي:
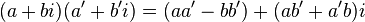
تتم عملية القسمة كما يلي:

الجذر التربيعي
انظر أيضا الجذر التربيعي للأعداد السالبة وللأعداد العقدية
الجذران التربيعيان للعدد العقدي a + bi (مع b ≠ 0) هما  حيث :
حيث :
 حيث :
حيث :
و
حيث sgn هي دالة الإشارة.
تمثيل الأعداد المركبة
إذا كان z عددا مركبا، و a و b عددين حقيقيين، و i هو الوحدة التخيلية، فمن الممكن تمثيل العدد المركب z كما يلي:
التمثيل الجبري
يكتب العدد المركب z جبريًا بالشكل:
التمثيل الهندسي
الأعداد المركبة بشكلها الجبري  لذا فكل عدد مركب هو زوج مرتب
لذا فكل عدد مركب هو زوج مرتب  في محور الأعداد, وكل زوج كهذا يمكن حساب إحداثياته بواسطة الزاوية المتكونة من التقاء محور
في محور الأعداد, وكل زوج كهذا يمكن حساب إحداثياته بواسطة الزاوية المتكونة من التقاء محور  مع الخط المستقيم الخارج من نقطة الأصل ويمر في الزوج
مع الخط المستقيم الخارج من نقطة الأصل ويمر في الزوج  , وأيضا بواسطة طول الخط المحصور بين
, وأيضا بواسطة طول الخط المحصور بين  و-
و- 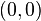 . هذه الإمكانية تسمح لنا بصياغة العدد المركب بالشكل التالي :
. هذه الإمكانية تسمح لنا بصياغة العدد المركب بالشكل التالي :
 لذا فكل عدد مركب هو زوج مرتب
لذا فكل عدد مركب هو زوج مرتب  في محور الأعداد, وكل زوج كهذا يمكن حساب إحداثياته بواسطة الزاوية المتكونة من التقاء محور
في محور الأعداد, وكل زوج كهذا يمكن حساب إحداثياته بواسطة الزاوية المتكونة من التقاء محور  مع الخط المستقيم الخارج من نقطة الأصل ويمر في الزوج
مع الخط المستقيم الخارج من نقطة الأصل ويمر في الزوج  , وأيضا بواسطة طول الخط المحصور بين
, وأيضا بواسطة طول الخط المحصور بين  و-
و- 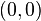 . هذه الإمكانية تسمح لنا بصياغة العدد المركب بالشكل التالي :
. هذه الإمكانية تسمح لنا بصياغة العدد المركب بالشكل التالي :
حيث:
التمثيل الأسي
يكتب العدد على شكل
حيث:
الخصائص
بنية الحقل
حلول المعادلات الحدودية
ليكن a0, …, an أعدادا مركبة (تسمى معاملات). للمعادلة
حل واحد على الأقل z، إذا افتُرض أنه على الأقل أحد الأعداد ذات الدرجات الأعلى، a1, …, an غير مساو للصفر. هذا هو نص المبرهنة الأساسية في الجبر. لهذا السبب، يُقال عن المجموعة C أنها حقل مغلق جبريا. هذه الخاصية ليست متوفرة في حقل الأعداد الجذرية Q (ليس لمتعددة الحدود x2 − 2 من جذر كسري بما أن حلها هو √2 و هو عدد غير كسري). مجموعة الأعداد الحقيقية R لا تمتلك هي أيضا هذه الخاصية (ليس لمتعددة الحدود x2 + a من جذر حقيقي عندما يكون a موجبا قطعا).
انظر إلى مبرهنة ليوفيل وإلى طوبولوجيا وإلى نظرية غالوا وإلى مصفوفة مربعة وإلى القيم الذاتية والمتجهات الذاتية.
الدوال التامة الشكل
يقال عن دالة f : C → C أنها دالة تامة الشكل إذا حققت معادلات كوشي-ريمان. على سبيل المثال، كل تحويل خطي C → C يكتب على الشكل :
حيث a و b عددان عقديان. يكون هذا التحويل كامل الشكل إذا وفقط إذا كان b مساويا للصفر.
لحق نقطة ولحق متجهة
المستوى 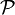 منسوب لمعلم متعامد، متجانس (ممنظم)
منسوب لمعلم متعامد، متجانس (ممنظم)  ، التطبيق الذي يربط كل عدد مركب
، التطبيق الذي يربط كل عدد مركب  جزؤه الحقيقي a وجزؤه التخيلي b بالنقطة M التي زوج احداثياتها
جزؤه الحقيقي a وجزؤه التخيلي b بالنقطة M التي زوج احداثياتها  من
من 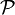 ، هو تطبيق تقابلي والعدد المركب
، هو تطبيق تقابلي والعدد المركب  يسمى 'لحق' النقطة M ويرمز له بالرمز
يسمى 'لحق' النقطة M ويرمز له بالرمز 
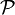 منسوب لمعلم متعامد، متجانس (ممنظم)
منسوب لمعلم متعامد، متجانس (ممنظم)  ، التطبيق الذي يربط كل عدد مركب
، التطبيق الذي يربط كل عدد مركب  جزؤه الحقيقي a وجزؤه التخيلي b بالنقطة M التي زوج احداثياتها
جزؤه الحقيقي a وجزؤه التخيلي b بالنقطة M التي زوج احداثياتها  من
من 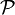 ، هو تطبيق تقابلي والعدد المركب
، هو تطبيق تقابلي والعدد المركب  يسمى 'لحق' النقطة M ويرمز له بالرمز
يسمى 'لحق' النقطة M ويرمز له بالرمز 
التطبيق الذي يربط كل عدد مركب جزؤه الحقيقي a وجزؤه التخيلي b بالمتجهة 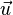 من
من 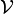 التي أفصولها a وأرتوبها b، هو تطبيق تقابلي والعدد المركب
التي أفصولها a وأرتوبها b، هو تطبيق تقابلي والعدد المركب  يسمى 'لحق' المتجهة
يسمى 'لحق' المتجهة 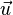 .
.
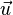 من
من 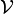 التي أفصولها a وأرتوبها b، هو تطبيق تقابلي والعدد المركب
التي أفصولها a وأرتوبها b، هو تطبيق تقابلي والعدد المركب  يسمى 'لحق' المتجهة
يسمى 'لحق' المتجهة 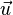 .
.نظرية الأعداد الجبرية
لكل معادلة حدودية غير ثابتة وذات معاملات مركبة، كما سبق ذكر ذلك، حل في C. هذه المسألة تبقى صحيحة حتى إذا كانت هؤلاء المعاملات أعدادا كسرية. جذور هذه المعادلات تسمى أعداد جبرية. تشكل الأعداد الجبرية موضوع دراسة أساسي في النظرية الجبرية للأعداد.
انظر إلى حقل (رياضيات) وإلى حقل الأعداد الجبرية وإلى جذور الوحدة (تحليل عقدي) وإلى تساعي (مضلع) وإلى إنشاءات الفرجار والمسطرة وإلى عدد طبيعي غاوسي وإلى مبرهنة فيرما حول مجموع مربعين.
نظرية الأعداد التحليلية
تدرس نظرية الأعداد التحليلية الأعداد الطبيعية والجذرية, مستغلة كونها قابلة للتمثيل على شكل أعداد عقدية. على سبيل المثال، ترتبط دالة زيتا لريمان ζ(s) بتوزيع الأعداد الأولية.
التاريخ
أول إشارة سريعة إلى الجذور المربعة للأعداد السالبة قد تعود إلى أعمال عالم الرياضيات الإغريقي هيرو السكندري, الذي عاش في القرن الأول بعد الميلاد.
انظر إلى جيرولامو كاردانو وإلى المبرهنة الأساسية في الجبر.



















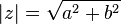










0 التعليقات:
إرسال تعليق