الاعداد الطبيعية
في الرياضيات، العدد الطبيعي (بالإنجليزية: Natural number) هو كل عدد صحيح موجب، مثل 1، 2، 3... 12، 563. ويضيف بعض العلماء الصفر إلى هذه المجموعة من الأعداد. يرمز لمجموعة الأعداد الطبيعية بالحرف اللاتيني N. و هي مجموعة أعداد غير منتهية. يمثل 1 أصغرها، ويتم إنشاؤها بواسطة علاقة الترجع: كل عدد طبيعي له موال وهو أيضا عدد صحيح طبيعي, 1 عدد صحيح طبيعي.
أي: "1 عدد طبيعي، وإذا كان  عدداً طبيعياً، فإن
عدداً طبيعياً، فإن 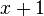 عدد طبيعي أيضاً."
عدد طبيعي أيضاً."
 عدداً طبيعياً، فإن
عدداً طبيعياً، فإن 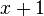 عدد طبيعي أيضاً."
عدد طبيعي أيضاً."
وكل مجموعة مرتبة تخضع لأكسيومات بيانو تسمى مجموعة أعداد طبيعية. ويُرمز إلى هذه المجموعة ب N أو يرمز إليها ب *N إذا حذف منها الصفر. بعض الرياضيين لا يعتبرون الصفر عددا صحيحا طبيعيا.
- ومن خصائصها الجبرية : الانغلاق بعمليتي الجمع والضرب
- التجميعة، الضرب عملية تجميعية: (c × b) × a = (c × b) × a.
- التبادلية، الجمع عملية تبديلية في مجموعة الأعداد الطبيعية: تغيير مكان الطرفين في العملية لا يغير النتيجة :a + b = b + a. الضرب عملية تبديلية في مجموعة الأعداد الطبيعية : تغيير مكان الطرفين في العملية لا يغير النتيجة : a × b = b × a.
- وجود العناصر المحايدة، صفر هو العنصر الحيادي لعملية الجمع في مجموعة الأعداد الطبيعية: النتيجة (أو الحاصل) بعد جمع عدد وصفر هو نفس العدد. a + 0 = a. الواحد (1) هو العنصر المحايد لعملية الضرب في مجموعة الأعداد الطبيعية: النتيجة (أو الحاصل) بعد ضرب عدد وواحد هو نفس العدد. a × 1 = a.
- توزيعية عملية الضرب على عملية الجمع في مجموعة الأعداد الطبيعية :a × (b + c) = a × b + a × c
- لا وجود لقواسم الصفر, إذا كان a و b عددين طبيعيين حيث 0 = a × b فإن a = 0 أو b = 0..
تاريخ الأعداد الطبيعية وما موقع الصفر ؟
لم يعتبر العديد من علماء الرياضيات الإغريق الواحد عددا. فبالنسبة إليهم، اثنان هو أصغر عدد.
الأعداد الزوجية والأعداد الفردية
العدد الصحيح إن كان له نصف صحيح أي غير منكسر فزوج، كالعشرة، وإلا ففرد، كالثلاثة. نقول أن عددان لهما نفس الزوجية سواء إذا كانا زوجيين معا أو فرديين معا.
- ينتج عن عملية الجمع أو الطرح بين عددين لهما نفس الزوجية، عدد زوجي.
- عدد زوجي + عدد زوجي = عدد زوجي، مثال:
 .
. - عدد فردي + عدد فردي = عدد زوجي، مثال:
 .
.
- عدد زوجي + عدد زوجي = عدد زوجي، مثال:
- ينتج عن عملية الجمع أو الطرح بين عددين ليس لهما نفس الزوجية، عدد فردي.
- عدد فردي + عدد زوجي = عدد فردي، مثال:
 .
.
- عدد فردي + عدد زوجي = عدد فردي، مثال:
- ينتج عن عملية الضرب بين عددين زوجيين، عدد زوجي. مثال:
 .
. - ينتج عن عملية الضرب بين عددين فرديين، عدد فردي. مثال:
 ي
ي - ينتج عن عملية الضرب بين عدد زوجي وعدد فردي، عدد زوجي. مثال:
 .
.
عملية القسمة تتعلق بالبسط والمقام:
- إذا كان البسط زوجياً والمقام فردياً سنحصل على عدد زوجي أو عدد كسري.
- أمثلة :
 .
.
- أمثلة :
- إذا كان البسط فردياً والمقام زوجياً سنحصل على عدد كسري دائماً.
- أمثلة:
 .
.
- أمثلة:
- إذا كان البسط والمقام زوجيين سنحصل على عدد زوجي أو عدد فردي أو عدد كسري.
- أمثلة:
 .
.
- أمثلة:
- إذا كان البسط والمقام فرديين سنحصل على عدد فردي أو عدد كسري.
- أمثلة:
 .
.
- أمثلة:







0 التعليقات:
إرسال تعليق